【雜談】「二元數」？

發表於 2020-03-18

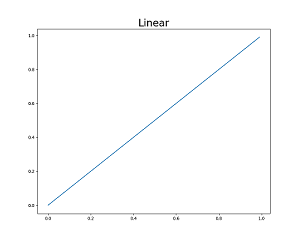
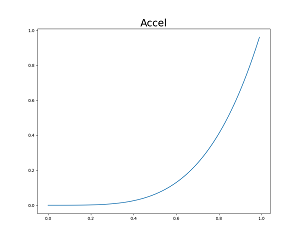
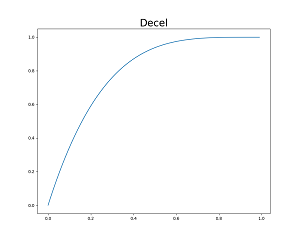
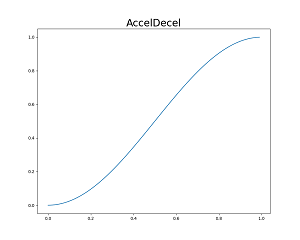
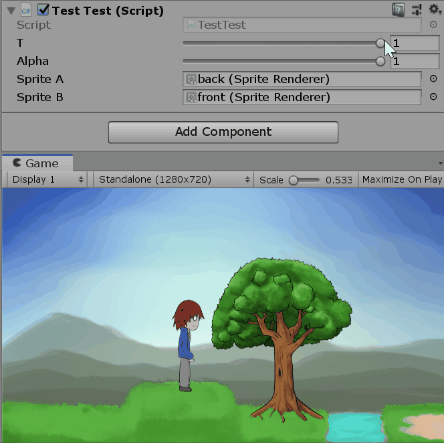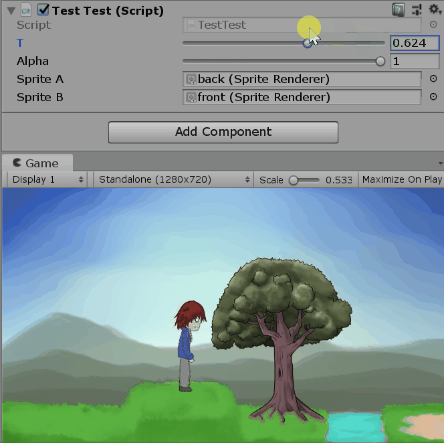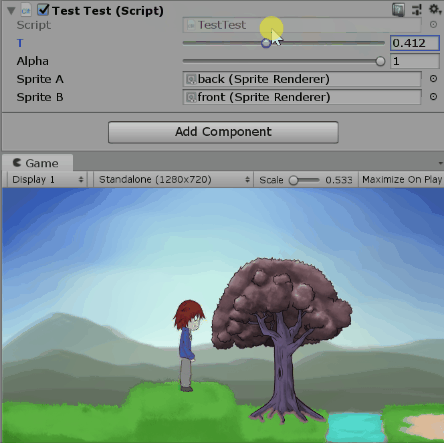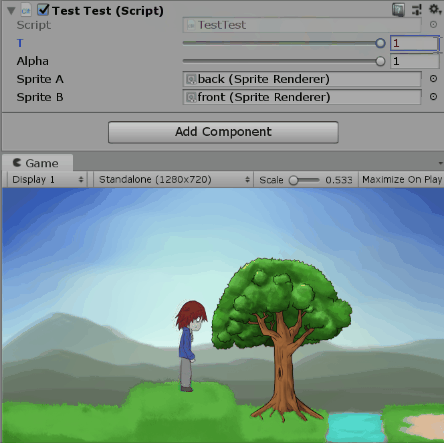
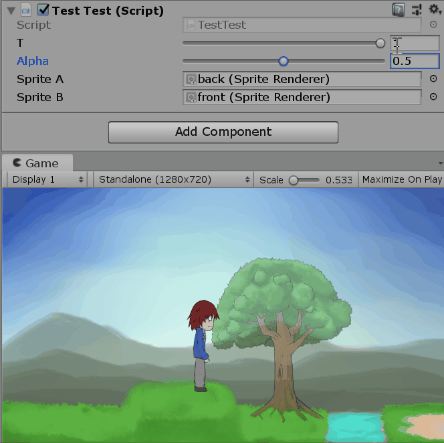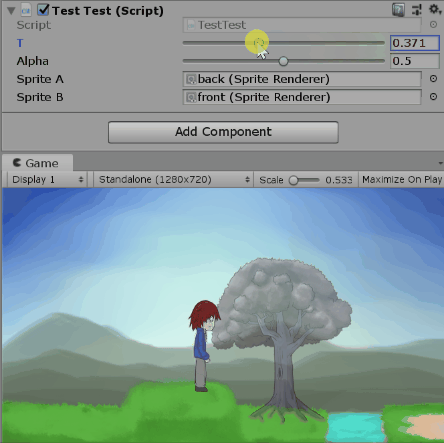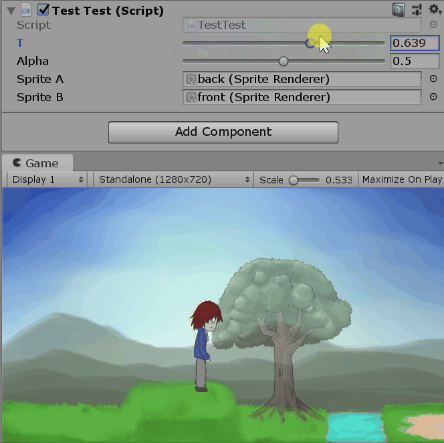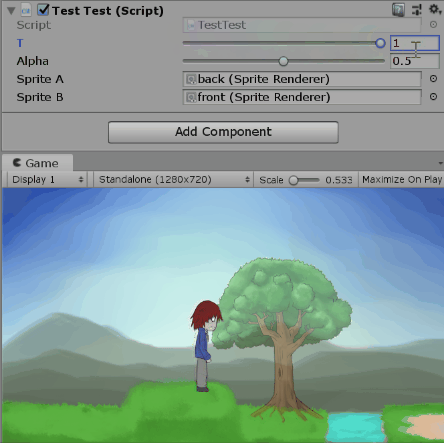
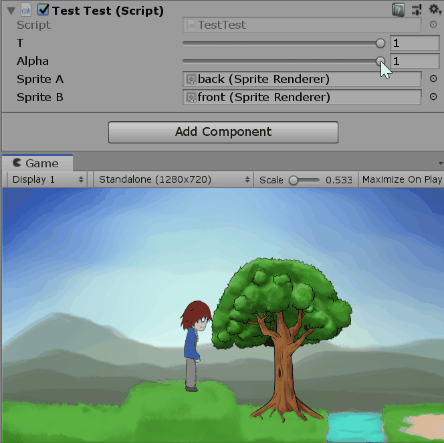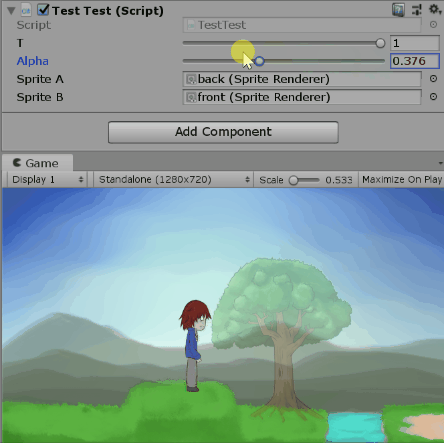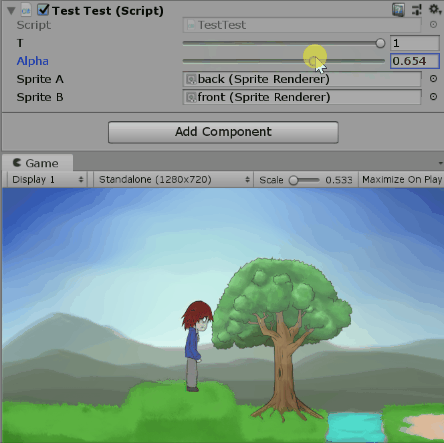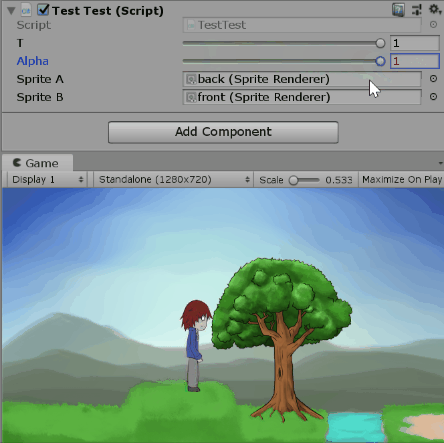
四元數可以表示三度空間的旋轉狀態，那你知道複數也可以表示二度空間的旋轉狀態嗎？

用四元數表示三度空間的旋轉狀態有很多好處。
其中一個最棒的點在於他不像用角度來內插，它並不會出現從359度轉到0度時，變成在繞遠路的狀況。
四元數內插走的永遠是兩個狀態間「最近」的旋轉。
因為太贊了，所以遊戲引擎通常都是用四元數來表示旋轉的。

於是我就在想，既然三度空間的旋轉有這麼方便的東西可以用，那二度空間呢？
結果…就找到了這個神奇的東西。

懶人包就是「複數可以表示二度空間的旋轉狀態」

說實在，我看過這東西後，覺得這根本就是自找麻煩。
因為二度空間的旋轉也就兩個方向，大不了用個判斷一下角度就知道該轉哪邊了。
就算退個一百步，用內建好的四元數也行啊，因為二維旋轉畢竟也是三維旋轉的一種。
但我覺得是一個很有趣的想法，而且它的原理跟四元數有異曲同工之妙，感覺了解它就有助於瞭解四元數。

這個方法的原理，是用複數平面上的單位向量來表示二度空間的旋轉狀態。
複數平面上，單位圓上的值都可以用這個形式表示：
$$z = e^{i\theta}$$

我的理解是，假如用在圓上0度的地方點一個紅點，那麼旋轉後這個點就會落在單位圓上的某處。
而且任一旋轉狀態下都恰好對應到該點在圓上一個可能的位置。
我猜這應該就是這個方法的出發點。

實作的方法，是先把角度轉代進上式，得到單位複數。
起始角度和終止角度各會給我們一個單位複數。
在兩個複數間做內插，再把內插值歸一化，就得到另一個單位複數。
這個方法相當於在起點跟終點所連成的圓弧間做內插，所以走的當然會是近的路。(應該吧)

不過要注意，直接用線性內插的話，旋轉速度非等速。(這點跟四元數內插非常類似！)
因此如果想要得到等速旋轉的話，還必須乘上一個權重才行。
至於權重怎麼算我就懶得看了，反正…誰會用這個鬼方法做2D旋轉啊。
等到我哪天去看四元數時再想辦法一起搞懂吧。

不過看完這篇後，我心裡還浮出了另一個疑問：
「為什麼用角度就可能會繞遠路，但用複數就可以？」
角度跟複數有甚麼本質上的區別，導致它們有這個差異？
於是我便開始了漫長的思考。

解釋1
角度的定義是從x軸開始逆時鐘旋轉的夾角。
可以比喻成「兩個旋轉狀態的差」。
打個比方，0度跟359度內插，其實變成是「逆時鐘轉0度」跟「逆時鐘轉359度」作內插。
因此才會出現看似繞遠路的行為。
而複數不一樣，它本身就是「旋轉狀態」。
因此它的內插就會是狀態的內插，會得到最近的結果。

解釋2
另一個解釋跟複數平面上的log的branch cut有關。
我們雖然可以用複數代表旋轉狀態，但最後如果要還原成角度，我們就得取log。
以剛才的式子來說：
$$z = e^{i\theta}$$
則
$$\theta = -i * log(z)$$
可是注意，這裡是沒辦法完全還原$\theta$的，因為複數平面的log並沒有辦法對應到所有可能的角度。
由於單位圓上的一個點有無數個角度對應到它 (一個角度加360度仍會對到同一點)
因此我們在取log時必須規定角度的範圍，例如-180~180度。
於是這邊就出現了一個尷尬的斷點。

這兩個解釋其實意思差不多：「角度是旋轉狀態的失真表示法」
嘛，或許真的是這樣也說不定。看來複數才是真正適合表示2D旋轉的載體？
不過就算這樣，下次做2D遊戲時處理旋轉時，我想我還是會選擇用角度加if判斷來實作吧…

【遊戲數學】內插法1 - 兩點間的內插

發表於 2020-03-16

簡介

內插法是一種用離散的數據點產生連續變化的辦法。
它是遊戲中最常見的數學工具之一。可以說沒有它的話，遊戲根本做不成。

舉個例子，骨架動畫的關鍵影格。
在作動畫時，只要定義好關鍵影格的角色動作，程式就會自動幫我們產生出中間的動作。
事實上，兩個關鍵影格之間的動作就是內插出來的。

換句話說，假如不用內插法，我們就得手動設定每一幀所有骨頭的角度。
作過的人應該知道這是多麼星爆的一件事…

不只是動畫，甚至連軌跡曲線、圖片的旋轉等等都是用內插實現的。
你能想像一張圖片得存各種旋轉角度、各種尺寸的版本嗎？
因此內插法節省了我們很多工夫以及記憶體。
它讓我們在記錄一連串連續過程時，不需要紀錄所有的中間狀態，只要紀錄幾個關鍵資料點就好。

今天因為是系列的第一篇，就先來介紹最簡單的情況，也就是兩點間的內插。
為了方便，接下來也都會以「內插函數」代稱「兩點間的內插函數」。

內插函數的性質

試著把一個滑順的動畫慢動作撥放看看，會發現每個影格間變化的程度都不會太大。
「滑順」在數學上其實就是連續的意思。指在很短的時間變化內，狀態也不會有太大的變化。
尋找兩點間的內插，其實就是在找一個通過兩點的連續函數。

先來定義一些等等會用到的變數：
起始值：s
終止值：d
時刻：t，介於0到1之間。

所謂的內插函數，就是一個函數f(s, d, t)。
給定「起始值」，「終止值」以及之間的「時刻」，輸出對應的「內插值」。
其中要符合以下三個條件：

t=0時，輸出為s
t=1時，輸出為d
函數連續

內插法在遊戲裡最常見的應用，就是讓t在一段時間內從0變成1，這樣函數的輸出值就會從s逐漸變化成d。
這使我們可以讓遊戲中的物件從一個狀態順暢的變化成另一個狀態。
無論是位移、變形、淡入淡出還是變色，都是建立在「平滑變化」的基礎上。

內插函數介紹

內插函數的種類非常多，因為他有很多可以調的性質。
比如是頭、中、尾的部分是要加速還是減速，陡峭還是平穩，要不要抖動…等等。
就像有很多配菜，每個都可以選擇加或不加一樣，組合出來的種類就非常多。
基本上各種場合都有最適合的內插函數。
甚至有人做了一個內插函數大抄的網頁來展示各種內插函數的效果。

由於遊戲中的內插往往是每幀都要計算一次，遊戲中的內插函數通常都很簡單。
大多都是多項式或常見函數的組合。
如果是3D建模的軟體，可能就會考慮稍微複雜的函數來讓形狀好看點。
例如3D曲面有時會使用NURBS函數。
這邊先來介紹幾個簡單又常見的。

線性內插
$$f(s, d, t) = s + (d-s)*t$$

毫無反應，就是一條線。
因為計算簡單，這是最常用的內插函數。
但它最大的缺點就是開始和結束都很突然，因此不適合在某些場合使用。
例如，位移動畫就不太適合。因為人眼對速度的變化很敏感。
但顏色的變化就還好，因此淡入淡出常常都是用線性內插來實作。

加速內插
$$f(s, d, t) = s + (d-s)*t^N$$

其中N越大加速的幅度越大。
由於結束的瞬間會忽然停下，通常是用來當滑出畫面的動畫。

減速內插
$$f(s, d, t) = s + (d-s)*(1-(1-t)^N)$$

其中N越大減速的幅度越大。
可以看出來其實就是很偷懶的把加速內插的圖形轉180度。
由於開始的瞬間很突然，通常會拿來做滑進畫面的動畫。

先加速後減速內插
$$f(s, d, t) = s + (d-s) * \frac{1+cos(\pi*(1+t))}{2} $$

他的名字叫AccelerateDecelerateInterpolator，可以說是Android開發者的惡夢。
名字長到驚天地泣鬼神，完美的展現為什麼大家討厭Java。
(我甚至懶得打這一串，這是直接從Android的頁面複製過來的)
這個函數很常被用來作位移動畫，因為他起始和結束時，速度都是剛好為零。
因此整個變化過程不僅值是連續的，連速度都是連續的，做出來的動畫看上去就很舒服。

歸一化

有些人應該已經看出來了，這些不同的內插函數其實有著相同的形式：
$$f(s, d, t) = s + (d-s)*g(t)$$
g(t)是一個介於0和1的函數。
也就是說我們其實可以將相同的部分提出，只留下g(t)，這個動作稱為歸一化。
歸一化後的內插函數稱作歸一內插函數。

歸一化帶給我們很多好處。
首先輸入和輸出的範圍都變成了0到1，處理起來很方便，無論怎麼迭代範圍都會固定在0和1之間。
因此我們可以任意組合兩個歸一內插函數，來得到另一個歸一內插函數。
並且，只要經過任意的縮放和平移，就可以把歸一內插函數變成任兩個值之間的內插函數。

以下是上面提到的內插函數的歸一化版本：

線性內插：
$$g(t) = t$$

加速內插：
$$g(t) = t^N$$

減速內插：
$$g(t) = 1-(1-t)^N$$

先加速後減速內插
$$g(t) = \frac{1+cos(\pi*(1+t))}{2} $$
(這個東西就算歸一化還是很醜)

程式實作

這邊以一個遊戲中最常碰到的內插動畫：「將物體從A點順暢的移到B點」
來示範Unity如何實作兩點內插函數，以及各個內插函數的使用效果。

Unity自己有實作未歸一化的線性內插函數，也就是有名的Mathf.Lerp。
他的形式如下：
$$Lerp(s, d, t) = s + (d-s)*t$$

這個形式感覺很熟悉…我們回頭看看剛才的「內插函數共通形式」
$$f(s, d, t) = s + (d-s)*g(t)$$
唯一的差別就只有t變成了g(t)。
事實上，只要把指定的歸一化內插函數g(t)塞進t的位置，它就變成原本的內插函數f(t)了。

因此實作兩點內插函數的方法，就是先實作各種歸一化內插函數，然後塞進Lerp裡就成了。
那麼我們就來實作剛剛提過的各種歸一化內插函數吧。

public static class Interpolator{
    // 線性內插函數
    public static float Linear(float t){
        return t;
    }	
    // 加速內插函數
    public static float Accel(float t){
        return Mathf.Pow(t, 4);
    }	
    // 減速內插函數
    public static float Decel(float t){
        return 1-Mathf.Pow(1-t, 4);
    }	
    // 先加速後減速內插函數
    public static float AccelDecel(float t){
        return (1+Mathf.Cos(Mathf.PI*(1+t)))*0.5f;
    }
}

接下來來實作內插動畫的函數。
用程式產生動畫，自然少不了coroutine。
這邊的實作方式是在指定的時間內，每個frame都計算目前時間對應到的內插值，再用內插值來更新物件狀態。
結束的時候再更新一次狀態，以確保結束的狀態正確。

public static class Interpolation
{
    public static IEnumerator Transition(float src, float dst, float duration, Func<float, float> interpolator, Action<float> onUpdate) {
        float time = 0;
        while (time < duration)
        {
            float t = interpolator(time/duration);
            float current = Mathf.Lerp(src, dst, t);
            onUpdate(current);
            time += Time.deltaTime;
            yield return null;
        }
        onUpdate(dst);
    }
}

src是初始值，dst是結束值，duration是動畫的長度。
這個函式會在給定的時間內使一個數值從src變化成dst。

這邊最重要的就是interpolator跟onUpdate兩個參數。
interpolator是我們想指定的歸一化內插函數。把它餵給Lerp後，就變成了任意兩個值之間的內插函數。
而onUpdate則負責更新遊戲物件的狀態，它會取得該時刻的內插值，再根據內插值來設定物件的狀態。

這邊補充一下，剛接觸C#的人可能看不太懂這兩個參數的型別。
這兩個參數實際上都是「函數」。
Action代表「參數是一個float的函數，沒有回傳值的函數」。
Func<float, float>代表「輸入是一個float，回傳值也是float函數」。

這邊之所以要大費周章的把函數從外面傳進來，而不是寫在內插動畫裡，是為了能重複利用Transition這個函數。
要是我們哪天不想作位移動畫了，而是想要做變色的動畫，
我們就只需要把onUpdate改成一個設定顏色的函數就好了，完全不用改Transition。
Action和Func都屬於Delegate的概念，以後有機會會在其他文章補充。

以下則是實際呼叫動畫函數的腳本。這個物件會在遊戲開始時，會從指定的起始位置移動到結束位置。

public class Player : MonoBehaviour {
    [SerializeField] private float _srcX;
    [SerializeField] private float _dstX;
    [SerializeField] private float _duration;

    void Start () {
        StartCoroutine(Interpolation.Transition(_srcX, _dstX, _duration, Interpolator.Linear, UpdatePosX));
    }
	
    private void UpdatePosX(float x)
    {
        Vector3 pos = transform.position;
        pos.x = x;
        transform.position = pos;
    }
}

為了方便，起始位置、結束位置和時間長都可以在編輯器裡設定。

這邊展示一下各個內插函數的移動效果。

線性內插：

加速內插：

減速內插：

先加速後減速內插：

進階補充：Delegate小技巧

如果你希望能設定加速和減速的幅度呢？
這邊可以寫成兩個變數。

public static float Accel(float t, float rate){
    return Mathf.Pow(t, rate);
}	

public static float Decel(float t, float rate){
    return 1-Mathf.Pow(1-t, rate);
}

但問題來了：interpolator參數的型別是Func<float, float>，不能塞兩個參數的函數。
這時我們可以用lambda包裝它

1	t => Accel(t, rate)

最後就變成：

public static float Accel(float t, float rate){
    return Mathf.Pow(t, rate);
}	

public static Func<float, float> Accel(float rate){
    return t => Accel(t, rate);
}	

public static float Decel(float t, float rate){
    return 1-Mathf.Pow(1-t, rate);
}	

public static Func<float, float> Decel(float rate){
    return t => Decel(t, rate);
}

使用上大概會是這樣：

1
2
3

void Start(){
    StartCoroutine(Transition(startPoint, endPoint, 3, Interpolator.Accel(3), UpdatePosX));
}

這裡代表使用了加速程度是3的加速內插函數。

補充

內插函數生成器：http://www.timotheegroleau.com/Flash/experiments/easing_function_generator.htm

支援中斷事件的Coroutine

發表於 2019-12-01

簡介

今天在處理上一代社長Prefab的遺產。

這是一個用Unity作的簡單的GalGame引擎，不過目前只有播放五句話的功能。
分別是「AAAAAAA」、「BBBBBBB」、「CCCCCCCCC」、「DDDDDD」
以及「EEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE」

為什麼最後一句特別長呢？因為我想要測試一個功能，那就是在播放台詞時如果玩家按了按鍵，
就會中斷文字的動畫，直接顯示整句話。所以要有一句特別長來讓我不耐煩。

顯示文字的動畫是一個coroutine。Prefab的做法是在StartCoroutine時把coroutine存在對話框的class裡面，
然後玩家如果在顯示到一半時按空白鍵，就直接呼叫StopCoroutine，然後直接顯示整句話。

這個方法確實可以做到，不過仔細想想，玩家輸入按鍵時中斷動畫這個功能在遊戲中實在太常用了。
因此我們會希望這個這個函式不是對話框獨有的，而是一個在函式庫裡的函式。
它可以把一個coroutine變成能夠靠按鍵中斷。並且在中斷時，會執行某個特定的函式來直接跳躍過程，直達結果。

跳躍過程，直達結果。

如果我們有緋紅之王的話，就可以很輕鬆地做到這件事情。可惜我們沒有，那就只好寫code了。

用StopCoroutine實作

我們來寫個class叫叫InputEventListener。顧名思義，就是一個會監聽玩家輸入的class。
它提供一個函式叫Run，玩家只要將coroutine跟中斷事件函式丟給它，它就會給你一個包裝好的，能中斷的coroutine。

Run的實作方式基本上就是把對話框裡的code照搬過來。
首先就是呼叫StartCoroutine並把Coroutine存起來…

…欸等一下，StartCoroutine是MonoBehaviour的函式，這邊沒辦法直接執行。

嗯，好吧。這邊必須新增一個MonoBehaviour的輸入參數。看來函數的樣子沒辦法像當初想得那樣簡潔。

1	public IEnumerator Run(MonoBehaviour mono, IEnumerator e, Action onInput);

接下來我們就在MonoBehaviour身上呼叫StartCoroutine，然後每個frame都檢查玩家是否有按下空白鍵。
如果玩家按下空白鍵，那麼我們就呼叫StopCoroutine，然後呼叫OnInput，也就是我們的中斷回呼函式。
如果沒有，就一直執行到coroutine結束為止。

這也很簡單，我們只要用一個while區段，然後一直看coroutine.IsFinished是否為true就好…

…欸等一下。

…Coroutine好像沒有這個變數。

……
冷靜，一定是我孤陋寡聞，記錯變數的名稱了。
畢竟Coroutine應該是包裝IEnumerator的class，理論上應該要有能夠知道是否結束的功能。
所以這時候當然就是要拿出工程師的兩大救星，google跟
StackOverflow(平抬)。

(google中)

結論。

還真他媽沒有。

…沒辦法了，只能自己開一個變數來偵測coroutine是否結束了。
這邊我們得再寫一個coroutine，在開始時將IsFinished設成false，然後結束時再設成true。
這樣就能用while迴圈偵測IsFinished然後進行處理了。

最後的實現如下：


public class InputEventListener
	bool _isFinished = false;
	Coroutine _coroutine = null;
	
	public InputEventListener(){}
	
	private IEnumerator _Run(IEnumerator e){
		_isFinished = false;
		yield return e;
		_isFinished = true;
	}
	
	public IEnumerator Run(MonoBehaviour mono, IEnumerator e, Action onInput){
		_coroutine = mono.StartCoroutine(_Run(e));
		while(!_isFinished){
			if(Input.GetKeyDown(KeyCode.Space)){
				mono.StopCoroutine(_coroutine);
				onInput.Invoke();
			}
			else{
				yield return null;
			}
		}
	}
}

總覺得複雜度有點超出一開始的想像了。

首先，需要的變數比想像中還要多。本來以為拿一個coroutine跟一個函式就好，
現在不但還要吃MonoBehaviour，還要自己處理IsFinished。

而且這個方法還需要一個class，變成我們在呼叫Run之前還得作出一個class才行。
這邊不得不用class是因為IsFinished我們要讓Run裡面能取得IsFinished，但我們會希望每個可中斷coroutine有自己的IsFinished。

可能有人想說用把_Run新增一個輸出參數就好了：

private IEnumerator _Run(IEnumerator e, out bool isFinished){
	isFinished = false;
	yield return e;
	isFinished = true;
}

但問題是coroutine是不能用out的。所以如果真的想要用輸入參數來取得IsFinished的話，我們還得用自己把bool包起來：

public class ResultHolder<T>{
	public T Result { get; set;}
}

...

private IEnumerator _Run(IEnumerator e, ResultHolder<bool> isFinished){
	isFinished.Result = false;
	yield return e;
	isFinished.Result = true;
}

怎麼感覺越寫越亂了，嘔嘔嘔嘔嘔。

這麼簡單的功能真的需要這麼複雜的方法實現嗎？

自己手動跑Coroutine來實現

我們回顧一下剛才碰到的麻煩。

輸入牽扯到MonoBehaviour，增加依賴。日後要擴增功能會有隱憂。
使用前還得實體化一個class，增加管理麻煩和記憶體負擔。

追根究柢，就是Unity內建的Coroutine太雞巴了。不但StartCoroutine強制綁在MonoBehaviour身上，
而且Coroutine看起來明明像一個把IEnumerator包好的class，卻連「是否已結束」這種基本的功能都沒實作。
氣氣氣氣氣。

為了尋求究極的解決方法，我只好去研究Unity是怎麼把IEnumerator拿來當Coroutine用的了。
然後經過一番研究，終於總結出了它的用法：

IEnumerator有MoveNext這個函式和Current這個變數。
Unity會不斷呼叫MoveNext來執行coroutine的程式碼，直到碰到yield敘述。
MoveNext如果回傳為true就代表coroutine還沒結束，反之就代表已經結束。
Unity會根據Current來決定要休息多久才繼續coroutine。

欸？…

MoveNext如果回傳為true就代表coroutine還沒結束，反之就代表已經結束。

這不就是我們要的嗎？

唉，果然上層沒有提供的功能還是得自己從底層實作啊，沒想到都到Unity9102了我還要說這句話。
不過總之，一個究極的可中斷coroutine總算誕生了：

public static IEnumerator RunAsInputEventListener(this IEnumerator coroutine, Action onConfirm)
{
	while (coroutine.MoveNext())
	{
		if (Input.GetKeyDown(KeyCode.Space))
		{
			onConfirm.Invoke();
			break;
		}
		else
		{
			yield return coroutine.Current;
		}
	}
	yield return null;
}

我們透過自行控制coroutine，來避免呼叫StartCoroutine的種種麻煩。
有了MoveNext後，我們就能確認coroutine是否結束了，不用自己實作IsFinished。除此之外邏輯都差不多。

最重要的，我們要完全模仿Unity使用coroutine的方式，才能讓我們要包裝的coroutine正常執行。
而模仿的最高境界就是叫Unity自己處理，所以yield return的地方我們直接回傳Current，讓Unity根據回傳值來判斷要休息多久。
例如最常用的yield return null，Unity會休息到下一個frame再繼續coroutine。
如果亂傳一通的話，有可能會發生永遠到達不了coroutine結束的事實。

最後一個細節就是結尾那個yield return null，這樣寫是為了不要按一次按鍵觸發兩個事件。
因為這個函式結束後可能還會有其他輸入偵測，但這時KeyDown還是true，
所以這邊只能多等一個frame，不然直接跑下去就會繼續觸發下一個對話。

以下是這個函式的一個使用範例：

IEnumerator PlayDialog(string name, string content)
{
	IEnumerator speaking = dialog.Speaking(content, name);
	yield return speaking.RunAsInputEventListener(() => { 
		dialog.printAll(content, name);
	});
	yield return InputEvent.WaitForInputEvent();
}

dialog.Speaking是顯示對話的動畫coroutine，它會一個字一個字的顯示對話。
呼叫RunAsInputEventListener後，會得到一個可中斷的coroutine，並且在中斷時直接printAll。

至於InputEvent.WaitForInputEvent則是單純的等待，在玩家輸入前不會做任何事。

玩家如果乖乖地等文字跑完，我們就等玩家按下空白鍵才播放下一個對話。
如果玩家在文字跑到一半就性急的按下空白鍵，則我們就直接將文字跑完，然後再等一次空白鍵才播放下一個對話。

這個實現方法既不用牽扯到MonoBehaviour，也不用實體化一個class，簡潔了很多。
而且用法起來也方便，它就只是把coroutine包裝成另一個coroutine，底層的coroutine長甚麼樣子都無所謂。
而且牽扯到的class不多，所以以後不太需要回來改。只有Input看起來是最危險的，但這個可以等日後再擴增。

於是，我們總算讓所有動畫都能使用中斷事件，Prefab的在天之靈也得已安息了。

參考資料

StackOverflow: Yield and coroutines, how do they actually work?
Unity協程（Coroutine）原理深入剖析再續

Alpha合成的錯誤打開方式

發表於 2019-11-24

簡介

Alpha合成是影像處理和遊戲裡很常見的功能。
利用alpha合成，可以將多張圖片合併到同一個畫面，也可以實現圖片的漸變。
例如在FlipTale裡，玩家執行「翻面」時，所有的背景圖都會變色。

不過新手在用alpha合成時，常常會因為不清楚原理而作出意料之外的結果。
就拿剛才那個「變色」當例子吧。假設我們想要將圖A漸變成圖B，該怎麼做？(圖層B的在圖層A前面)
很多人會這麼作：

將圖A的alpha值從1漸變成0
將圖B的alpha值從0漸變成1

但很抱歉，如果這樣寫的話，在漸變到一半(50%)時你就會看到這個畫面：

樹變成透明了，嗚嗚嗚嗚嗚。

Alpha合成的原理

哪裡出錯了？漸變到一半的時候圖A和圖B的alpha值都是50%，那麼不是應該是AB各半嗎？
為了知道為什麼出錯，我們得來了解一下alpha合成的原理。

首先alpha合成的數學公式為：
$$ c = \alpha \cdot c_f + (1-\alpha) \cdot c_b $$
其中c是最終的顏色，$c_f$是前景色，$c_b$是背景色，$\alpha$則是alpha值。
可以看出來，alpha合成的運作方式是「將背景色和前景色以加權的方式混合」。
前景色的權重是$\alpha$，而背景色的權重是$1-\alpha$。

然後重點來了：每次電腦繪製一張圖片的時候，它會將圖片與背景作alpha合成。
並且「混合的結果會寫入背景，作為下一次alpha合成的背景色」。

光這樣講可能還是難以想像，那麼我們實際來套套看alpha合成的公式，來檢查剛才出錯的例子吧。

首先，電腦繪製出背景。
接下來畫圖A，圖A的alpha值是0.5，因此電腦將前景與背景以各50%的比例混合。
因此這時的結果是「50%背景色、50%圖A顏色」。
接下來再繪製圖B，圖B的Alpha也是0.5，因此電腦將前景與背景以各50%的比例混合。
但因為現在的背景是剛才混合的結果，因此最終的結果是「50%圖B、25%圖A、25%背景」。

發現了嗎？背景並沒有消失，他還有25%。所以我們才會看到背景。

漸變參數

我們換個角度來思考。
會出現這個錯誤，其實是因為alpha值實在太不直觀了，導致我們很容易想錯。
我們不如試試看用人腦比較能理解的數值來取代alpha值。

Alpha合成的順序是「圖A跟背景混合」，再來「圖B跟剛才的結果混合」。
假設改成「圖A跟圖B混合」，再「將剛才的結果跟背景混合」，是不是直觀多了？
因此我們這邊來定義新的參數吧。

漸變度t
代表合成圖是比較接近圖A還是圖B。圖A擁有1-t的權重，圖B則擁有t的權重。

整體透明度$\alpha$
代表「整張合成圖」的alpha值。也就是說，合成圖擁有$\alpha$的權重，背景色擁有$1-\alpha$的權重。

這個方法的好處是，我們可以把圖A跟圖B當成一張圖來思考。
我們只需要管這張圖的alpha值，以及它介於圖A跟圖B之間的係數就好，比兩個alpha值容易理解得多。

實現方法

用t跟$\alpha$作為參數，等於是改變計算alpha合成的順序。
也就是先用t作為alpha值，將圖A跟圖B作第一次合成，再用$\alpha$作為alpha值，將混合圖跟背景進行第二次合成。

但問題是我們沒辦法改變alpha合成的順序啊？我們該怎麼用t跟alpha來兜出我們要的混合圖呢？

方法有兩個。

第一個方法很簡單，寫shader就可以了。

拜託，現在已經有ShaderGraph，讓你不用寫code就可以作shader了，可以不要這樣看我嗎？
不過事實上當初我寫FlipTale時我也不會shader，因此今天就是要分享當初我是怎麼解決的。

第二個方法，簡單來說就是硬爆。

我們知道，不寫shader是不可能改變alpha合成的規則的。
那麼如果我們知道我們想要的圖A、圖B、背景的比例，能不能用這個比例來倒推出那兩個機車的alpha該設多少，圖片才會看起來跟我們想的一樣呢？

首先我們把需要的參數都列出來：
$c_a$：圖A的顏色
$c_b$：圖B的顏色
$\alpha_a$：圖A的alpha值
$\alpha_b$：圖B的alpha值
$b$：背景色

我們的目標是用t跟%\alpha%解出$\alpha_a$跟$\alpha_b$。

首先，我們用t跟$\alpha$算出我們想要的圖A、圖B、背景顏色的比例。

先將圖A跟圖B混合：
$$ c_1 = (1-t) \cdot c_a + t \cdot c_b $$
再將剛才的結果跟背景混合：
$$ c_2 = \alpha \cdot c_1 + (1-\alpha) \cdot b $$
將$c_1$代進來，得到：
$$ c_2 = (1-t)\alpha \cdot c_a + t \alpha \cdot c_b + (1-\alpha) \cdot b $$

接下來，我們來計算標準的alpha合成，圖A、圖B、背景各自的比例：

先將圖A跟背景混合：
$$ c_1 = \alpha_a \cdot c_a + (1-\alpha_a) \cdot b $$
再將圖B跟剛才的結果混合：
$$ c_2 = \alpha_b \cdot c_b + (1-\alpha_b) \cdot c_1 $$
整理一下，得到
$$ c_2 = \alpha_a (1-\alpha_b) \cdot c_a + \alpha_b \cdot c_b + (1-\alpha_a)(1-\alpha_b) \cdot b $$

來比較兩次的結果吧。為了能夠用t跟$\alpha$精確控制顏色的比例，兩次的結果中$c_a$跟$c_b$和$b$前面乘的係數必須相等。

$c_a$係數相等，給我們這個條件：
$$ (1-t) \alpha = \alpha_a(1-\alpha_b)$$
$c_b$係數相等，給我們這個條件：
$$ t \alpha = \alpha_b$$

背景色還會給我們一條方程式，但因為未知數只有兩個，所以兩條式子就夠了。
然後一看第二條式子，發現…$\alpha_b$已經自動被解出來了，爽啊.jpg。
$$ \alpha_b = t \alpha$$
代回去第一條式子，解出$\alpha_a$
$$ \alpha_a = \frac{(1-t) \alpha}{(1-t \alpha)}$$

最後，我們就得到用t跟$\alpha$來表示$\alpha_a$跟$\alpha_b$的公式了。
$$ \alpha_a = \frac{(1-t) \alpha}{(1-t \alpha)}, \quad \alpha_b = t \alpha$$