簡介
Alpha合成是影像處理和遊戲裡很常見的功能。
利用alpha合成,可以將多張圖片合併到同一個畫面,也可以實現圖片的漸變。
例如在FlipTale裡,玩家執行「翻面」時,所有的背景圖都會變色。

不過新手在用alpha合成時,常常會因為不清楚原理而作出意料之外的結果。
就拿剛才那個「變色」當例子吧。假設我們想要將圖A漸變成圖B,該怎麼做?(圖層B的在圖層A前面)
很多人會這麼作:
將圖A的alpha值從1漸變成0
將圖B的alpha值從0漸變成1
但很抱歉,如果這樣寫的話,在漸變到一半(50%)時你就會看到這個畫面:

樹變成透明了,嗚嗚嗚嗚嗚。
Alpha合成的原理
哪裡出錯了?漸變到一半的時候圖A和圖B的alpha值都是50%,那麼不是應該是AB各半嗎?
為了知道為什麼出錯,我們得來了解一下alpha合成的原理。
首先alpha合成的數學公式為:
$$ c = \alpha \cdot c_f + (1-\alpha) \cdot c_b $$
其中c是最終的顏色,$c_f$是前景色,$c_b$是背景色,$\alpha$則是alpha值。
可以看出來,alpha合成的運作方式是「將背景色和前景色以加權的方式混合」。
前景色的權重是$\alpha$,而背景色的權重是$1-\alpha$。
然後重點來了:每次電腦繪製一張圖片的時候,它會將圖片與背景作alpha合成。
並且「混合的結果會寫入背景,作為下一次alpha合成的背景色」。
光這樣講可能還是難以想像,那麼我們實際來套套看alpha合成的公式,來檢查剛才出錯的例子吧。
首先,電腦繪製出背景。
接下來畫圖A,圖A的alpha值是0.5,因此電腦將前景與背景以各50%的比例混合。
因此這時的結果是「50%背景色、50%圖A顏色」。
接下來再繪製圖B,圖B的Alpha也是0.5,因此電腦將前景與背景以各50%的比例混合。
但因為現在的背景是剛才混合的結果,因此最終的結果是「50%圖B、25%圖A、25%背景」。
發現了嗎?背景並沒有消失,他還有25%。所以我們才會看到背景。
漸變參數
我們換個角度來思考。
會出現這個錯誤,其實是因為alpha值實在太不直觀了,導致我們很容易想錯。
我們不如試試看用人腦比較能理解的數值來取代alpha值。
Alpha合成的順序是「圖A跟背景混合」,再來「圖B跟剛才的結果混合」。
假設改成「圖A跟圖B混合」,再「將剛才的結果跟背景混合」,是不是直觀多了?
因此我們這邊來定義新的參數吧。
漸變度t
代表合成圖是比較接近圖A還是圖B。圖A擁有1-t的權重,圖B則擁有t的權重。
整體透明度$\alpha$
代表「整張合成圖」的alpha值。也就是說,合成圖擁有$\alpha$的權重,背景色擁有$1-\alpha$的權重。
這個方法的好處是,我們可以把圖A跟圖B當成一張圖來思考。
我們只需要管這張圖的alpha值,以及它介於圖A跟圖B之間的係數就好,比兩個alpha值容易理解得多。
實現方法
用t跟$\alpha$作為參數,等於是改變計算alpha合成的順序。
也就是先用t作為alpha值,將圖A跟圖B作第一次合成,再用$\alpha$作為alpha值,將混合圖跟背景進行第二次合成。
但問題是我們沒辦法改變alpha合成的順序啊?我們該怎麼用t跟alpha來兜出我們要的混合圖呢?
方法有兩個。
第一個方法很簡單,寫shader就可以了。

拜託,現在已經有ShaderGraph,讓你不用寫code就可以作shader了,可以不要這樣看我嗎?
不過事實上當初我寫FlipTale時我也不會shader,因此今天就是要分享當初我是怎麼解決的。
第二個方法,簡單來說就是硬爆。
我們知道,不寫shader是不可能改變alpha合成的規則的。
那麼如果我們知道我們想要的圖A、圖B、背景的比例,能不能用這個比例來倒推出那兩個機車的alpha該設多少,圖片才會看起來跟我們想的一樣呢?
首先我們把需要的參數都列出來:
$c_a$:圖A的顏色
$c_b$:圖B的顏色
$\alpha_a$:圖A的alpha值
$\alpha_b$:圖B的alpha值
$b$:背景色
我們的目標是用t跟%\alpha%解出$\alpha_a$跟$\alpha_b$。
首先,我們用t跟$\alpha$算出我們想要的圖A、圖B、背景顏色的比例。
先將圖A跟圖B混合:
$$ c_1 = (1-t) \cdot c_a + t \cdot c_b $$
再將剛才的結果跟背景混合:
$$ c_2 = \alpha \cdot c_1 + (1-\alpha) \cdot b $$
將$c_1$代進來,得到:
$$ c_2 = (1-t)\alpha \cdot c_a + t \alpha \cdot c_b + (1-\alpha) \cdot b $$
接下來,我們來計算標準的alpha合成,圖A、圖B、背景各自的比例:
先將圖A跟背景混合:
$$ c_1 = \alpha_a \cdot c_a + (1-\alpha_a) \cdot b $$
再將圖B跟剛才的結果混合:
$$ c_2 = \alpha_b \cdot c_b + (1-\alpha_b) \cdot c_1 $$
整理一下,得到
$$ c_2 = \alpha_a (1-\alpha_b) \cdot c_a + \alpha_b \cdot c_b + (1-\alpha_a)(1-\alpha_b) \cdot b $$
來比較兩次的結果吧。為了能夠用t跟$\alpha$精確控制顏色的比例,兩次的結果中$c_a$跟$c_b$和$b$前面乘的係數必須相等。
$c_a$係數相等,給我們這個條件:
$$ (1-t) \alpha = \alpha_a(1-\alpha_b)$$
$c_b$係數相等,給我們這個條件:
$$ t \alpha = \alpha_b$$
背景色還會給我們一條方程式,但因為未知數只有兩個,所以兩條式子就夠了。
然後一看第二條式子,發現…$\alpha_b$已經自動被解出來了,爽啊.jpg。
$$ \alpha_b = t \alpha$$
代回去第一條式子,解出$\alpha_a$
$$ \alpha_a = \frac{(1-t) \alpha}{(1-t \alpha)}$$
最後,我們就得到用t跟$\alpha$來表示$\alpha_a$跟$\alpha_b$的公式了。
$$ \alpha_a = \frac{(1-t) \alpha}{(1-t \alpha)}, \quad \alpha_b = t \alpha$$
測試與驗證

嗯…解出來是很棒啦,不過我們怎麼知道對不對?
我們大可寫個code來測試結果對不對,但我們姑且先代個簡單的數字進去檢查看看吧。
這邊只檢查一個情況,那就是alpha=1時,背景是否絕對不會透出來。
把alpha=1代進去上面的公式,得到:
$$ \alpha_a = 1, \quad \alpha_b = t $$
也就是說,如果我們只希望作漸變(t=0 -> t=1),我們圖A的alpha值應該從頭到尾都是1。
這很合理,因為只要圖A的alpha值不是1,那我們將圖A跟背景混合時背景就會透出來,這麼一來我們作漸變時無論如何都無法避免背景透出來。
既然看起來還算對(?),我們就用程式來驗證吧。以下是調整t跟$\alpha$的一些畫面。
測試alpha=1時改變t:
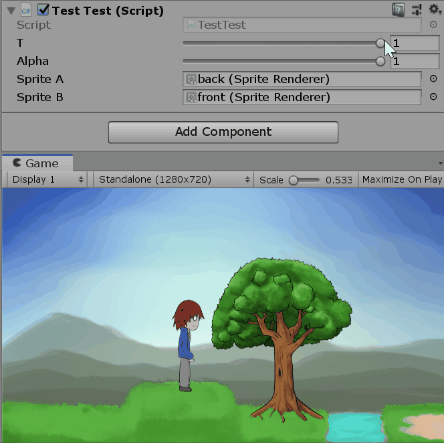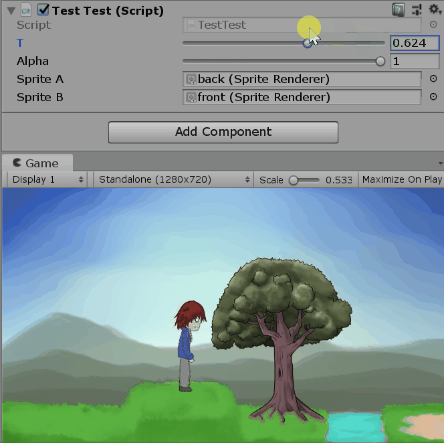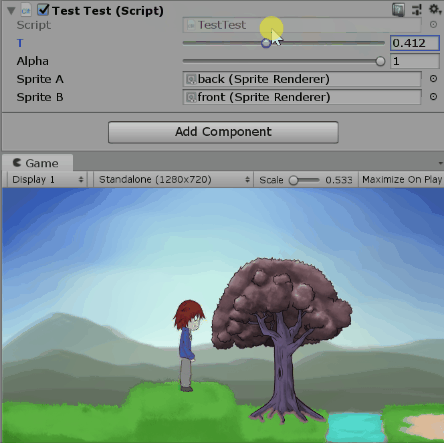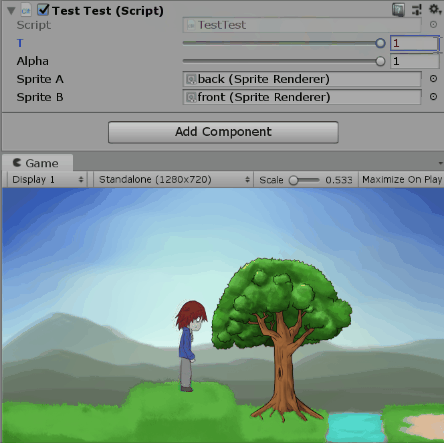
測試alpha=0.5時改變t:
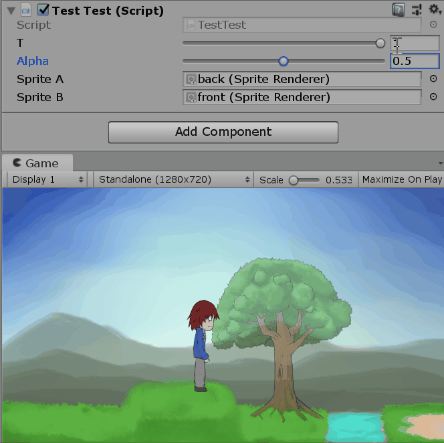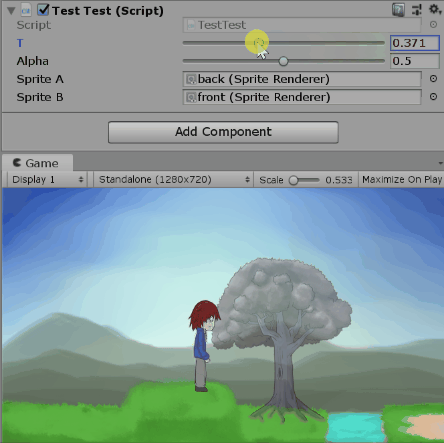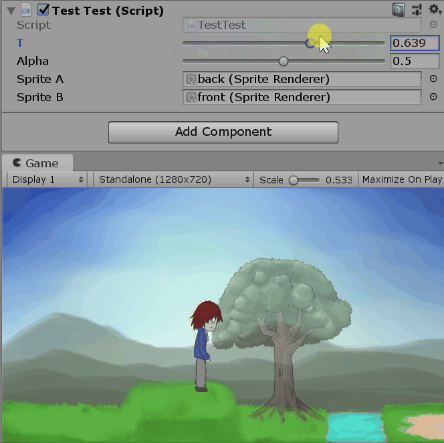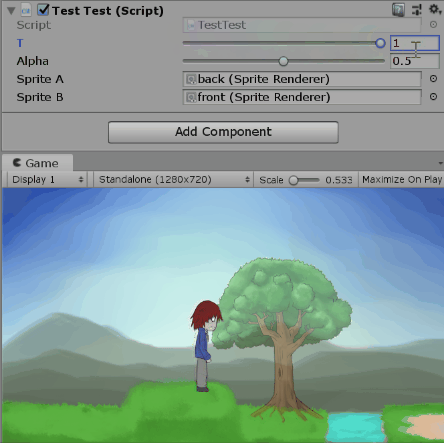
測試t=1時改變alpha:
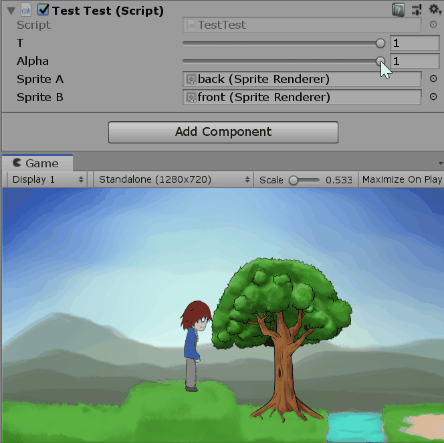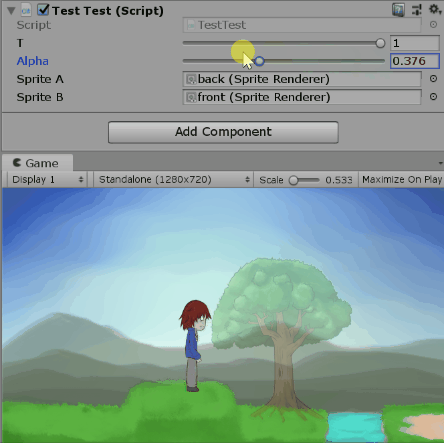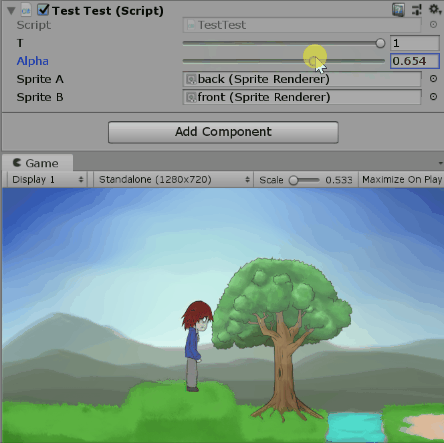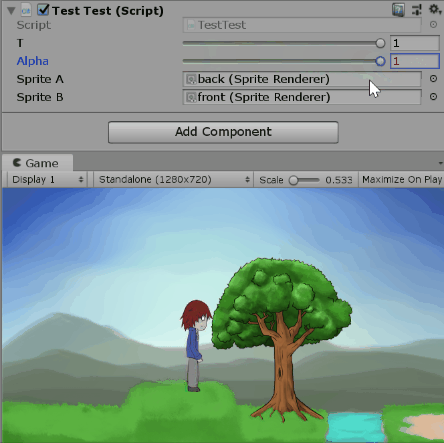
這樣就可以用t跟$\alpha$控制圖片的混合程度了。
結論:
這個故事告訴我們,一定要學shader。
否則哪一天要是你要調整10張圖片的比例,你就要算半天那個奇怪的公式……